. .

Autor(en)

  • Stephan Kulla ()

Lizenz

Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du

  • das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
  • Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen

Zur Verwendung musst du folgende Bedingungen einhalten:

  • Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.

Sei im Folgenden 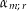$\curve{m}{r}$ die Kreiskurve mit Mittelpunkt 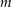$m$ und Radius $r$. Es sei also $\curve mr :\ \left[0,\,1\right]\rightarrow\C:\ t\mapsto m+r\cdot\exp\left(2\pi t \i\right)$. Berechne nun folgende Kurvenintegrale:

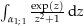  • $\int_\curve{1}{1} \frac{\exp\left(z\right)}{z^2+1} \dz$ (keine Definitionslücken innerhalb der zu integrierenden Kurve)

    Hinweis zum 1. Lösungsweg

    Überlege dir genau, auf welcher Menge die Funktion 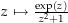$z\mapsto \frac{\exp\left(z\right)}{z^2+1}$ definiert (und damit analytisch) ist. Überlege dir auch, wie auf dieser Menge integriert wird.

    Lösungsweg 1.

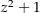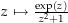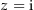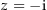    Der Nenner $z^2+1$ der Funktion $z\mapsto \frac{\exp\left(z\right)}{z^2+1}$ ist genau dann 0, wenn $z=\i$ oder $z=-\i$ ist. Damit ist der (maximale) Definitionsbereich von 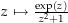$z\mapsto \frac{\exp\left(z\right)}{z^2+1}$ gleich 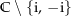$\C\setminus\left\{\i,\,-\i\right\}$. Auf dieser Menge ist die Funktion als Verknüpfung analytischer Funktionen wieder analytisch. Wenn du dir nun noch überlegst, über welche Kurve integriert wird, so kommst du zu folgendem Ergebnis: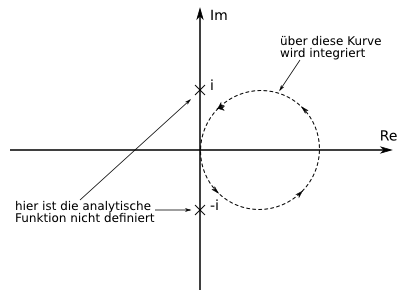

    Du siehst, dass die Kreisscheibe 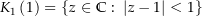$K_1\left(1\right) = \left\{ z\in\C:\ \amount{z-1}\lt 1\right\}$, um dessen Rand integriert wird, ganz im Definitionsbereich der zu integrierenden und analytischen Funktion 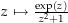$z\mapsto \frac{\exp\left(z\right)}{z^2+1}$ liegt (innerhalb der zu integrierenden Kurve gibt es also keine Definitionslücken). Wir können nun den Definitionsbereich so geschickt einschränken, dass dieser ein Sterngebiet ist und die zu integriende Kurve enthält. So erfüllt der Definitionsbereich 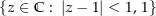$\left\{ z\in\C:\ \amount{z-1}\lt 1,\,1\right\}$ diese Eigenschaften: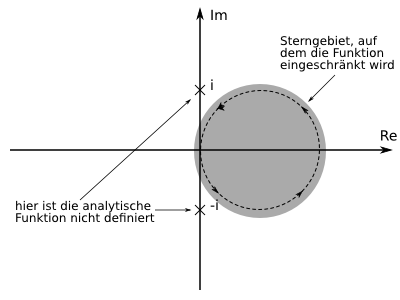

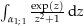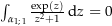    Wir können also $\int_\curve{1}{1} \frac{\exp\left(z\right)}{z^2+1} \dz$ als geschlossene Kurve einer auf einem Sterngebiet definierten analytischen Funktion auffassen. Da aber jedes geschlossene Kurvenintegral einer auf einem Sterngebiet definierten, analytischen Funktion gleich 0 ist (Cauchyscher Integralsatz für Sterngebiete), ist auch $\int_\curve{1}{1} \frac{\exp\left(z\right)}{z^2+1} \dz=0$.

    Hinweis zum 2. Lösungsweg

    Erweitere die zu integrierende Funktion 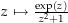$z\mapsto \frac{\exp\left(z\right)}{z^2+1}$ so, dass die Cauchysche Integralformel angewandt werden kann.

    Lösungsweg 2.

    Es ist


    \begin{align*}& \int_{\curve 11} \frac{\exp\left(z\right)}{z^2+1} \dz \\[4px] & {\color{Orange} \left\downarrow \frac{\exp\left(z\right)\cdot \left(z-1\right)}{\left(z^2+1\right)\cdot \left(z-1\right)} \text{ ist auf ganz } \curve 11 \text{ definiert, weil } 1\notin\curve 11 \right.}\\[4px] = & \int_{\curve 11} \frac{\exp\left(z\right)\cdot \left(z-1\right)}{\left(z^2+1\right)\cdot \left(z-1\right)} \dz \\[4px] = & \int_{\curve 11} \underbrace{\frac{\exp\left(z\right)\cdot \left(z-1\right)}{\left(z^2+1\right)}}_{=:\ \,\,f\left(z\right)} \cdot\frac{1}{z-1} \dz \\[4px] = & \int_{\curve 11} f\left(z\right) \cdot\frac{1}{z-1} \dz \\[4px] & {\color{Orange} \left\downarrow \begin{matrix} \text{Cauchysche Integralformel: } 2\pi\i f\left(x\right) = \int_{\curve 11} f\left(z\right) \cdot \frac{1}{z-x} dz \text{ f{\" u}r } x=1 \\[4px] \text{(anwendbar, weil sich innerhalb von } \curve 11 \text{ keine Definitionsl{\" u}cken befinden)} \end{matrix} \right.}\\[4px] = & 2\pi\i f\left(1\right) \\[4px] & {\color{Orange} \left\downarrow f\left(z\right) = \frac{\exp\left(z\right)\cdot \left(z-1\right)}{\left(z^2+1\right)} \right.}\\[4px] = & 2\pi\i \frac{\exp\left(1\right)\cdot \overbrace{\left(1-1\right)}^{=\,\,0}}{\left(1^2+1\right)} = 0 \\[4px]\end{align*}

  • $\i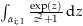nt_\curve{\i}{1} \frac{\exp\left(z\right)}{z^2+1} \dz$ (eine Definitionslücke innerhalb der zu integrierenden Kurve)

    Hinweis zum Lösungsweg

    Cauchysche Integralformel

    Lösungsweg

    Anders als in der obigen Aufgabe, liegt hier eine Definitionslücke innerhalb der zu integrierenden Kurve. Dies zeigt nochmal die folgende Skizze:

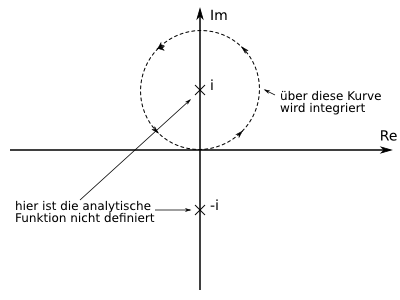
    Damit lässt sich der Cauchysche Integralsatz direkt verwenden:


    \begin{align*}& \int_\curve{\i}{1} \frac{\exp\left(z\right)}{z^2+1} \dz \\[4px] = & \int_\curve{\i}{1} \frac{\exp\left(z\right)}{\left(z+\i\right)\left(z-\i\right)} \dz \\[4px] = & \int_\curve{\i}{1} \underbrace{\frac{\exp\left(z\right)}{z+\i}}_{=:\ \,\,f\left(z\right)} \cdot \frac{1}{z-\i} \dz \\[4px] = & \int_\curve{\i}{1} f\left(z\right) \cdot \frac{1}{z-\i} \dz \\[4px] & {\color{Orange} \left\downarrow \begin{matrix} \text{Cauchysche Integralformel: } 2\pi\i f\left(x\right) = \int_{\curve{\i}{1}} f\left(z\right) \cdot \frac{1}{z-x} dz \text{ f{\" u}r } x=\i \\[4px] \text{(anwendbar, weil sich innerhalb von } \curve 11 \text{ keine Definitionsl{\" u}cken von } f\left(z\right) \text{ befinden)} \end{matrix} \right.}\\[4px] = & 2\pi\i f\left(\i\right) \\[4px] & {\color{Orange} \left\downarrow f\left(z\right) = \frac{\exp\left(z\right)}{z+\i} \right.}\\[4px] = & 2\pi\i \frac{\exp\left(\i\right)}{\i+\i} = \pi\exp\left(\i\right) \\[4px]\end{align*}

  • $\i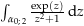nt_\curve{0}{2} \frac{\exp\left(z\right)}{z^2+1} \dz$ (mehrere Definitionslücken innerhalb der zu integrierenden Kurve)

    Hinweis zum 1. Lösungsweg

    Wende die Partialbruchzerlegung auf 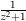$\frac{1}{z^2+1}$ an.

    Lösungsweg 1.

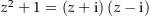    Wegen $z^2+1=\left(z+\i\right)\left(z-\i\right)$ erhalten wir für die Partialbruchzerlegung von 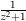$\frac{1}{z^2+1}$ den Ansatz 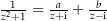$\frac{1}{z^2+1}=\frac{a}{z+\i}+\frac{b}{z-\i}$. Es ist


    \begin{align*}& \frac{1}{z^2+1}=\frac{a}{z+\i}+\frac{b}{z-\i} \\[4px] & {\color{Orange} \left\downarrow \cdot \left(z+\i\right) \right.}\\[4px] \Rightarrow\ & \underbrace{\frac{z+\i}{z^2+1}}_{=\frac{1}{z-\i}} = a +\frac{\left(z+\i\right)b}{z-\i} \\[4px] \Rightarrow\ & \frac{1}{z-\i} = a +\frac{\left(z+\i\right)b}{z-\i} \\[4px] & \text{ Setze } z=-\i \\[4px] \Rightarrow\ & \frac{1}{-\i-\i} = a + \frac{\overbrace{\left(-\i+\i\right)}^{=\ 0} b}{-\i-\i} \\[4px] \Rightarrow\ & a= \frac{1}{-2\i} = \frac{\i}{2} \\[4px]\end{align*}

    Analog erhalten wir für $b$


    \begin{align*}& \frac{1}{z^2+1}=\frac{a}{z+\i}+\frac{b}{z-\i} \\[4px] & {\color{Orange} \left\downarrow \cdot \left(z-\i\right) \right.}\\[4px] \Rightarrow\ & \underbrace{\frac{z-\i}{z^2+1}}_{=\frac{1}{z+\i}} = \frac{\left(z-\i\right)\cdot a}{z+\i} + b \\[4px] \Rightarrow\ & \frac{1}{z+\i} = \frac{\left(z-\i\right)\cdot a}{z+\i} + b \\[4px] & \text{ Setze } z=\i \\[4px] \Rightarrow\ & \frac{1}{\i+\i} = \frac{\overbrace{\left(\i-\i\right)}^{=\ 0}\cdot a}{\i+\i} + b \\[4px] \Rightarrow\ & b= \frac{1}{2\i} = -\frac{\i}{2} \\[4px]\end{align*}

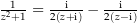    Damit ist $\frac{1}{z^2+1}=\frac{\i}{2\left(z+\i\right)}-\frac{\i}{2\left(z-\i\right)}$. Nun können wir diese Partialbruchzerlegung bei der Integration anwenden und die zweite Teilaufgabe anwenden


    \begin{align*}& \int_\curve{0}{2} \frac{\exp\left(z\right)}{z^2+1} \dz \\[4px] = & \int_\curve{0}{2} \exp\left(z\right) \cdot \left(\frac{\i}{2\left(z+\i\right)}-\frac{\i}{2\left(z-\i\right)}\right) \dz \\[4px] = & \int_\curve{0}{2} \left(\frac{\i\cdot \exp\left(z\right)}{2\left(z+\i\right)}-\frac{\i\cdot\exp\left(z\right)}{2\left(z-\i\right)}\right) \dz \\[4px] = & \int_\curve{0}{2} \frac{\i\cdot \exp\left(z\right)}{2\left(z+\i\right)} \dz - \int_\curve{0}{2} \frac{\i\cdot\exp\left(z\right)}{2\left(z-\i\right)} \dz \\[4px] = & \int_\curve{0}{2} \frac{\i\cdot \exp\left(z\right)}{2}\cdot \frac{1}{z+\i} \dz - \int_\curve{0}{2} \frac{\i\cdot\exp\left(z\right)}{2}\cdot \frac{1}{z-\i} \dz \\[4px] & {\color{Orange} \left\downarrow \text{ selber L{\" o}sungsweg wie in der 2. Teilaufgabe} \right.}\\[4px] = & 2\pi\i \frac{\i\cdot \exp\left(-\i\right)}{2} - 2\pi\i \frac{\i\cdot\exp\left(\i\right)}{2} \\[4px] = & 2\pi\i \left(-\frac{\exp\left(-\i\right)}{2\i} + \frac{\cdot\exp\left(\i\right)}{2\i}\right) \\[4px] = & 2\pi\i \underbrace{\frac{\exp\left(\i\right)-\exp\left(-\i\right)}{2\i}}_{=\ \sin\left(\i\right)} \\[4px] = & 2\pi\i \sin\left(\i\right) \\[4px]\end{align*}

    Lösungsweg 2.

    Diese Aufgabe kann auch auch dadurch gelöst werden, indem geschickt integriert wird. Betrachte dazu folgende Skizze:

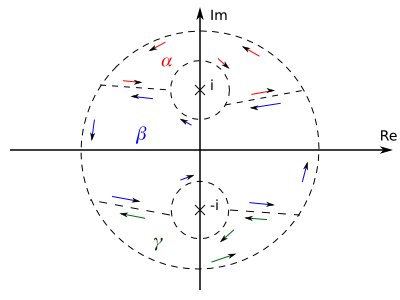
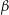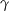    Wie bereits in der ersten Teilaufgabe gezeigt, sind die Kurvenintegrale über $\alpha$, $\beta$ und $\gamma$ gleich 0, weil es innerhalb dieser Kurve keine Definitionslücken gibt. Es ist also 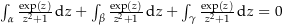$\int_\alpha \frac{\exp\left(z\right)}{z^2+1} \dz + \int_\beta \frac{\exp\left(z\right)}{z^2+1} \dz + \int_\gamma \frac{\exp\left(z\right)}{z^2+1} \dz =0$. Da sich dabei die Integration über die Verbindungsstrecken aufheben erhalten wir.


    \begin{align*}\int_{\curve 02}\frac{\exp\left(z\right)}{z^2+1} \dz = &\int_{\curve{\i}{1}}\frac{\exp\left(z\right)}{z^2+1} \dz + \int_{\curve{-\i}{1}}\frac{\exp\left(z\right)}{z^2+1} \dz \\[4px] & {\color{Orange} \left\downarrow \text{2. Teilaufgabe} \right.}\\[4px] = & 2\pi\i \cdot\frac{\exp\left(\i\right)}{\i+\i} + 2\pi\i \cdot\frac{\exp\left(\i\right)}{-\i-\i} \\[4px] = & 2\pi\i \cdot\left(\frac{\exp\left(\i\right)}{2\i} - \frac{\exp\left(-\i\right)}{2\i}\right) \\[4px] = & 2\pi\i \cdot\frac{\exp\left(\i\right)-\exp\left(-\i\right)}{2\i} = 2\pi\i\cdot\sin\left(\i\right) \\[4px]\end{align*}