. .
Aufgabe 1:

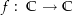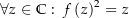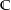Beweise, dass es keine stetige Funktion $f:\ \C\rightarrow\C$ mit der Eigenschaft $\forall z\in\C:\ f\left(z\right)^2=z$ gibt (es gibt also keine stetige Wurzelfunktion auf $\C$).