Aufgabe 1:
Man zeige: Ist 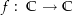 eine analytische Funktion und gibt es eine reelle Zahl
eine analytische Funktion und gibt es eine reelle Zahl 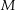 , so dass
, so dass 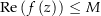 für alle
für alle 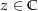 , dann ist
, dann ist 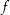 eine konstante Funktion (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 94)
eine konstante Funktion (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 94)
Das Bild einer nichtkonstanten, ganzen Funktion ist dicht in 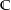 . (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 96)
. (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 96)