Beweise folgende Eigenschaften komplexer Kurvenintegrale
Das Kurvenintegral ist
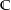 -linear. Das heißt es gilt
-linear. Das heißt es gilt 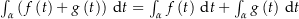 für glatte Kurven
für glatte Kurven ![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png) und stetige Funktionen
und stetige Funktionen ![$f,\,g:\ \alpha\left(\left[a,\,b\right]\right)\rightarrow\C$](img/60_423959671_080206060901a4080506a006020808a4.png) . Außerdem gilt
. Außerdem gilt 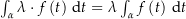 .
.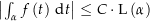 , wenn
, wenn 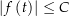 für alle
für alle 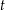 im Bild von
im Bild von 
Sei ![$\alpha:\ \left[0,\,1\right]\rightarrow\C:\ t\mapsto \exp\left(2\pi\i t\right)$](img/79_1341387861_03a50802a3010701a001050303a2a002.png) . Beweise, dass
. Beweise, dass 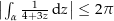 .
.
Beweise, dass das Kurvenintegral transformationsinvariant ist, dass also gilt: Sei ![$\alpha:\ \left[c,\,d\right]\rightarrow \C$](img/43_1702730020_04090804a0a20101a202090504a5a401.png) eine stückweise glatte Funktion und
eine stückweise glatte Funktion und ![$f:\ \alpha\left(\left[c,\,d\right]\right)\rightarrow\C$](img/56_-106820272_04a0a0a0a4a102040400a306a2a102a2.png) eine stetige Funktion. Sei nun
eine stetige Funktion. Sei nun ![$\phi:\ \left[a,\,b\right]\rightarrow\left[c,\,d\right]$](img/56_-1807124572_09a002a509050607a403a3a308070201.png) eine stetig differenzierbare Funktion mit
eine stetig differenzierbare Funktion mit 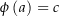 und
und 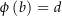 . Zeige, dass
. Zeige, dass 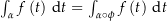
Beweise folgende Eigenschaft komplexer Integrale: Sei 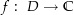 eine stetige Funktion (
eine stetige Funktion (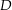 offen), die eine Stammfunktion
offen), die eine Stammfunktion 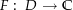 besitzt. So gilt für jede in
besitzt. So gilt für jede in 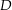 verlaufende glatte Kurve
verlaufende glatte Kurve ![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png) :
: 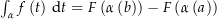
Berechne das Kurvenintegral 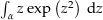 , wenn (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 68)
, wenn (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 68)
 die Verbinungssterecke zwischen
die Verbinungssterecke zwischen 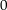 und
und 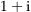 ist.
ist. die Verbindungsstrecke auf der Parabel von
die Verbindungsstrecke auf der Parabel von 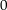 bis
bis 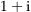 ist
ist
Beweise: Für eine stetige Funktion 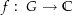 (
(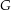 ist ein Gebiet) sind folgende Aussagen äquivalent
ist ein Gebiet) sind folgende Aussagen äquivalent
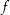 besitzt eine Stammfunktion
besitzt eine Stammfunktion- Jedes Kurvenintegral über
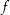 entlang einer geschlossenen Kurve
entlang einer geschlossenen Kurve  in
in 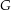 ist gleich
ist gleich 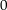 .
. - Jedes Kurvenintegral über
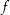 hängt nur vom Anfangs- und Endpunkten ab.
hängt nur vom Anfangs- und Endpunkten ab.
Beweisen sie, dass die komplexe Konjugation 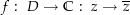 auf jeder nichtleeren und offenen Menge
auf jeder nichtleeren und offenen Menge 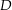 keine holomorphe Stammfunktion besitzt.
keine holomorphe Stammfunktion besitzt.