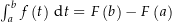Aufgabe 1:
Beweisen sie folgende Eigenschaften komplexer Integrale.
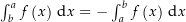
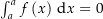
Das komplexe Integral ist
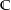 -linear. Das heißt, es ist
-linear. Das heißt, es ist 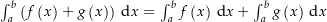 für alle
für alle ![$f,\,g :\ \left[a,\,b\right] \rightarrow \C$](img/45_728063657_a5a3a20906030004a20708a207a30309.png) und
und 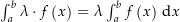 für alle
für alle 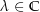 und
und ![$f:\ \left[a,\,b\right]\rightarrow \C$](img/38_125635644_0003a509a204a008a4a3a308a108a309.png) .
.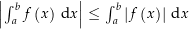
Beweise folgende Eigenschaften komplexer Integrale
Ist
![$F:\ \left[a,\,b\right]\rightarrow\C$](img/37_356442910_a40503a4040308a0a202000208080800.png) eine Stammfunktion von
eine Stammfunktion von 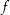 (also
(also 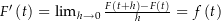 ), so ist
), so ist