Aufgabe 1:
Sei 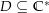 ein Gebiet, das den Nullpunkt nicht enthält. Eine stetige Funktion
ein Gebiet, das den Nullpunkt nicht enthält. Eine stetige Funktion 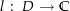 mit
mit 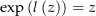 für alle
für alle 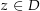 heißt stetiger Zweig des Logarithmus . Man zeige folgende Aussagen (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 85)
heißt stetiger Zweig des Logarithmus . Man zeige folgende Aussagen (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 85)
Jeder weitere stetige Zweig des Logarithmus
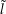 auf
auf 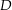 besitzt die Form
besitzt die Form 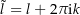
Jeder stetige Zweig ist
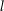 des Logarithmus ist sogar analytisch und es gilt
des Logarithmus ist sogar analytisch und es gilt 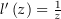
Auf
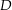 existiert genau dann ein stetiger Zweig des Logarithmus, wenn die Funktion
existiert genau dann ein stetiger Zweig des Logarithmus, wenn die Funktion  eine Stammfunktion auf
eine Stammfunktion auf 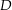 besitzt.
besitzt.