Quelle der Aufgabe
Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 85
Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Sei 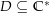 ein Gebiet, das den Nullpunkt nicht enthält. Eine stetige Funktion
ein Gebiet, das den Nullpunkt nicht enthält. Eine stetige Funktion 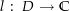 mit
mit 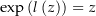 für alle
für alle 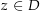 heißt stetiger Zweig des Logarithmus . Man zeige folgende Aussagen (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 85)
heißt stetiger Zweig des Logarithmus . Man zeige folgende Aussagen (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 85)
Jeder weitere stetige Zweig des Logarithmus
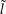 auf
auf 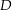 besitzt die Form
besitzt die Form 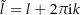
Sei
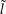 ein weiterer stetiger Zweig des Logarithmus und
ein weiterer stetiger Zweig des Logarithmus und 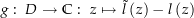 . Damit ist
. Damit ist 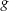 eine stetige Funktion. Außerdem ist
eine stetige Funktion. Außerdem ist![\begin{align*}& \exp\left(g\left(z\right)\right) = \exp\left(\tilde l\left(z\right)-l\left(z\right)\right) = \frac{\exp\left(\tilde l\left(z\right)\right)}{\exp\left(l\left(z\right)\right)} = \frac{z}{z} = 1 \\[4px] \Rightarrow \ & \exists k \in \Z:\ g\left(z\right)=2k\pi\i\end{align*}](img/292_1986699502_a1a5a3a1060204000807a00200a1a5a3.png)
Also ist
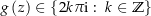 für alle
für alle 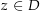 . Da
. Da 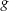 stetig ist, existiert für alle
stetig ist, existiert für alle 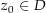 ein
ein 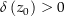 mit
mit 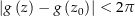 für alle
für alle  in der Umgebung
in der Umgebung 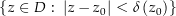 von
von 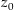 . Da
. Da 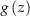 als Werte nur ganzzahlige Vielfache von
als Werte nur ganzzahlige Vielfache von 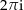 annehmen kann, besitzen 2 verschiedene Funktionswerte von
annehmen kann, besitzen 2 verschiedene Funktionswerte von 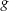 mindestens den Abstand
mindestens den Abstand 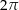 . Somit ist wegen
. Somit ist wegen 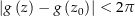 sogar
sogar 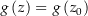 für alle
für alle 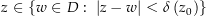 .
.Damit ist
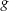 lokal konstant. Weil
lokal konstant. Weil 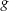 auf einem Gebiet definiert ist, ist
auf einem Gebiet definiert ist, ist 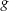 konstant (Auf Gebieten sind lokal konstante Funktionen konstant). Es existiert also ein
konstant (Auf Gebieten sind lokal konstante Funktionen konstant). Es existiert also ein 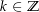 mit
mit 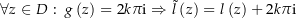 .
.Jeder stetige Zweig ist
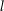 des Logarithmus ist sogar analytisch und es gilt
des Logarithmus ist sogar analytisch und es gilt 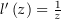
Zunächst gilt
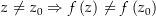 , denn es ist
, denn es ist![\begin{align*}& f\left(z\right) = f\left(z_0\right) \\[4px] \Rightarrow\ &\exp\left(f\left(z\right)\right)=\exp\left(f\left(z_0\right)\right) \\[4px] \Rightarrow\ &z=z_0 \\[4px]\end{align*}](img/199_184716014_00a0a4040401070306a2a3a207a00703.png)
Damit ist
![\begin{align*}l^\prime\left(z_0\right) & = \lim_{z\rightarrow z_0,\, z\ne z_0} \frac{f\left(z_0\right)-f\left(z\right)}{z_0-z} \\[4px] & = \lim_{z\rightarrow z_0,\, z\ne z_0} \frac{f\left(z_0\right)-f\left(z\right)}{\exp\left(f\left(z_0\right)\right)-\exp\left(f\left(z\right)\right)} \\[4px] & {\color{Orange} \left\downarrow \text{ es ist immer } f\left(z_0\right)-f\left(z\right) \ne 0 \text{ (siehe oben)} \right.}\\[4px] & = \lim_{z\rightarrow z_0,\, z\ne z_0} \left(\frac{\exp\left(f\left(z_0\right)\right)-\exp\left(f\left(z\right)\right)}{f\left(z_0\right)-f\left(z\right)}\right)^{-1} \\[4px] & {\color{Orange} \left\downarrow \lim_{z\rightarrow z_0} f\left(z\right) = f\left(z_0\right) \text{, weil f stetig ist} \right.}\\[4px] & = \left(\exp^\prime\left(f\left(z_0\right)\right)\right)^{-1} = \left(\exp\left(f\left(z_0\right)\right)\right)^{-1} = \frac{1}{z_0} \\[4px]\end{align*}](img/920_190782698_a10909050602a101a5a2a508a207a305.png)
Auf
 existiert genau dann ein stetiger Zweig des Logarithmus, wenn die Funktion
existiert genau dann ein stetiger Zweig des Logarithmus, wenn die Funktion  eine Stammfunktion auf
eine Stammfunktion auf  besitzt.
besitzt.Die erste Implikation wurde bereits in der obigen Teilaufgabe gezeigt. Es ist noch zu beweisen, dass, wenn es eine holomorphe Stammfunktion von
 auf
auf  gibt, es auch einen stetigen (und damit analytischen Zweig) auf
gibt, es auch einen stetigen (und damit analytischen Zweig) auf 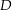 gibt. Sei im Folgenden also
gibt. Sei im Folgenden also 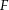 eine holomorphe Funktion mit Ableitung
eine holomorphe Funktion mit Ableitung  . Es ist
. Es ist![\begin{align*}& \left(\exp\left(F\left(z\right)\right)\cdot\frac{1}{z}\right)^\prime = \exp\left(F\left(z\right)\right)\cdot\frac{1}{z^2}-\exp\left(F\left(z\right)\right)\cdot\frac{1}{z^2}=0 \\[4px] \Rightarrow\ & z\mapsto\exp\left(F\left(z\right)\right)\cdot\frac{1}{z} \text{ ist konstant } \\[4px] \Rightarrow\ & \exp\left(F\left(z\right)\right)\cdot\frac{1}{z} = c \\[4px] \Rightarrow\ & \exp\left(F\left(z\right)\right) = c\cdot z \\[4px] & {\color{Orange} \left\downarrow c \ne 0 \text{, weil } \forall z \in D:\ \exp\left(F\left(z\right)\right)\ne 0 \right.}\\[4px] \Rightarrow\ & \exp\left(F\left(z\right)-\Log\left(c\right)\right) = z \\[4px]\end{align*}](img/689_831163759_0803a1a4a401a2060502000002a109a2.png)
Damit ist
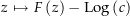 ein anayltischer (und damit stetiger) Zeig des Logarithmus auf
ein anayltischer (und damit stetiger) Zeig des Logarithmus auf 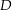 (Hier ist
(Hier ist 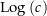 irgendeine komplexe Zahl mit
irgendeine komplexe Zahl mit 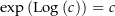 ).
).