. .

Autor(en)

  • Stephan Kulla ()

Lizenz

Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du

  • das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
  • Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen

Zur Verwendung musst du folgende Bedingungen einhalten:

  • Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.

Beweise, dass es keine stetige Funktion 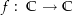$f:\ \C\rightarrow\C$ mit der Eigenschaft 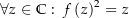$\forall z\in\C:\ f\left(z\right)^2=z$ gibt (es gibt also keine stetige Wurzelfunktion auf $\C$).

Hinweis zum Lösungsweg

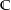Betrachte die Funktion 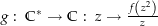$g:\ \Cunit\rightarrow\C:\ z\rightarrow \frac{f\left(z^2\right)}{z}$.

Lösungsweg

Es reicht hier aus zu beweisen, dass es keine stetige Wurzelfunktion 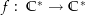$f:\ \Cunit\rightarrow\Cunit$ gibt. Denn, wenn es keine stetige Wurzelfunktion 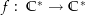$f:\ \Cunit\rightarrow\Cunit$ gibt, so kann es erst recht keine stetige Wurzelfunktion 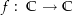$f:\ \C\rightarrow\C$ geben.

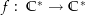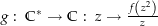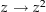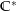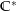Sei nun $f:\ \Cunit\rightarrow\Cunit$ eine stetige Wurzelfunktion und sei $g:\ \Cunit\rightarrow\C:\ z\rightarrow \frac{f\left(z^2\right)}{z}$ (Diese Abbildung ist wohldefiniert, weil unter der Abbildung $z\rightarrow z^2$ die Menge $\Cunit$ auf $\Cunit$ abgebildet wird). 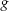$g$ ist damit als Verknüpfung stetiger Funktionen wieder eine stetige Funktion. Nun ist aus der Algebra bekannt, dass 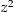$z^2$ genau zwei Wurzeln besitzt, nämlich $z$ und $-z$. 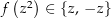Damit ist also $f\left(z^2\right)\in\left\{z,\,-z\right\}$ bzw. 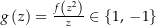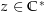$g\left(z\right)=\frac{f\left(z^2\right)}{z}\in\left\{1,\,-1\right\}$ für alle $z\in\Cunit$.

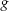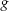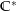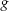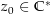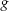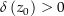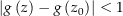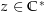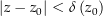Aufgrund der Stetigkeit von $g$ kann man zeigen, dass $g$ lokal konstant ist (dass es also um jeden Punkt auf $\Cunit$ eine Umgebung gibt, auf der $g$ konstant ist): Sei also $z_0\in\Cunit$ beliebig. Es ist $g$ stetig und es gibt damit ein $\delta\left(z_0\right) \gt 0$, so dass $\amount{g\left(z\right)-g\left(z_0\right)}\lt 1$ für alle $z\in\Cunit$ mit $\amount{z-z_0}\lt\delta\left(z_0\right)$. 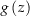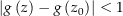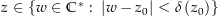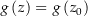Weil für $g\left(z\right)$ nur die Werte 1 und -1 in Frage kommen und $\amount{g\left(z\right)-g\left(z_0\right)}\lt 1$ für $z\in\left\{w\in\Cunit:\ \amount{w-z_0}\lt\delta\left(z_0\right)\right\}$ ist, ist $g\left(z\right)=g\left(z_0\right)$ für alle 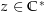$z\in\Cunit$ in der Umgebung 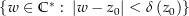$\left\{w\in\Cunit:\ \amount{w-z_0}\lt\delta\left(z_0\right)\right\}$ von $z_0$. 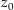Damit ist 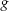$g$ eine lokal konstante Funktion.

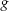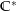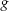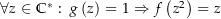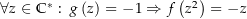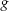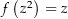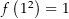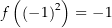Weil $g$ eine auf einer zusammenhängenden Menge $\Cunit$ definierte und lokal konstante Funktion ist, ist $g$ konstant und es gilt $\forall z\in\Cunit:\ g\left(z\right)=1\Rightarrow f\left(z^2\right)=z$ oder $\forall z\in\Cunit:\ g\left(z\right)=-1\Rightarrow f\left(z^2\right)=-z$. Sei nun oBdA $g$ konstant 1 und damit $f\left(z^2\right)=z$. Es ist also $f\left(1^2\right)=1$ und $f\left(\left(-1\right)^2\right)=-1$. 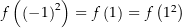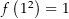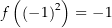Jedoch ist $f\left(\left(-1\right)^2\right)=f\left(1\right)=f\left(1^2\right)$, was ein Widerspruch zu $f\left(1^2\right)=1$ und $f\left(\left(-1\right)^2\right)=-1$ darstellt.