Quelle der Aufgabe
Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 96
Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Das Bild einer nichtkonstanten, ganzen Funktion ist dicht in 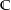 . (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 96)
. (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 96)
Beweis durch Kontraposition: Sei 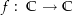 eine ganze Funktion, deren Bild
eine ganze Funktion, deren Bild 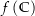 nicht dicht in
nicht dicht in 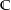 liegt. Zu zeigen ist, dass dann
liegt. Zu zeigen ist, dass dann 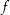 eine konstante Funktion ist.
eine konstante Funktion ist.
Wenn das Bild von 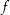 nicht dicht in
nicht dicht in 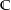 liegt, so ist dies äquivalent dazu, dass es eine komplexe Zahl
liegt, so ist dies äquivalent dazu, dass es eine komplexe Zahl 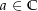 und eine Umgebung
und eine Umgebung 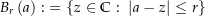 mit
mit 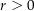 gibt, so dass
gibt, so dass 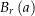 nicht im Bild
nicht im Bild 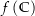 liegt (also
liegt (also 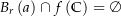 ). Nun definieren wir
). Nun definieren wir 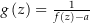 . Weil
. Weil 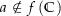 , ist
, ist 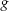 auf ganz
auf ganz 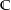 definiert (und dort als Verknüpfung analytischer Funktionen wieder analytisch).
definiert (und dort als Verknüpfung analytischer Funktionen wieder analytisch).
Nun ist 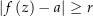 , weil
, weil 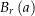 nicht im Bild von
nicht im Bild von 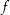 liegt. Also ist
liegt. Also ist 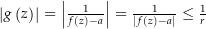 . Somit ist
. Somit ist 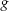 eine beschränkte Funktion und nach dem Satz von Liouville damit konstant. Es gilt also
eine beschränkte Funktion und nach dem Satz von Liouville damit konstant. Es gilt also
![\begin{align*}& g\left(z\right) = c \\[4px] \Rightarrow\ & \frac{1}{f\left(z\right)-a} = c \\[4px] & {\color{Orange} \left\downarrow c\ne 0 \text{, weil } \frac{1}{f\left(z\right)-a} \ne 0 \right.}\\[4px] \Rightarrow\ & f\left(z\right)-a = \frac{1}{c} \\[4px] \Rightarrow\ & f\left(z\right) = \frac{1}{c}+a = \const \\[4px]\end{align*}](img/351_-292851918_05010106a50205a50203a302a4090602.png)