Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Beweisen sie folgende Eigenschaften komplexer Integrale.
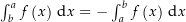
![\begin{align*}\int_b^a f\left(x\right) \dx & \defeq \underbrace{\int_b^a \Re\left(f\left(x\right)\right) \dx}_\text{reelles Integral} + \i \underbrace{\int_b^a \Im\left(f\left(x\right)\right) \dx}_\text{reelles Integral} \\[4px] & {\color{Orange} \left\downarrow \text{Nach Eigenschaft reeller Integrale} \right.}\\[4px] & = -\int_a^b \Re\left(f\left(x\right)\right) \dx + \i \left(-\int_a^b \Im\left(f\left(x\right)\right) \dx\right) \\[4px] & = -\left(\int_a^b \Re\left(f\left(x\right)\right) \dx + \i \int_a^b \Im\left(f\left(x\right)\right) \dx\right) \\[4px] & \defeq - \int_a^b f\left(x\right) \dx\end{align*}](img/635_-1349308734_07a205a4a0a5a40106a10705a10507a2.png)
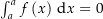
![\begin{align*}\int_a^a f\left(x\right) \dx & \defeq \underbrace{\int_a^a \Re\left(f\left(x\right)\right) \dx}_{=0} + \i \underbrace{\int_a^a \Im\left(f\left(x\right)\right) \dx}_{=0} \\[4px] & = 0 + \i \cdot 0 = 0\end{align*}](img/230_1256833496_040603a304a405060103a4a2a300a1a0.png)
Was passiert, wenn du die erste Eigenschaft auf
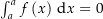 anwendest?
anwendest?![\begin{align*}& \int_a^a f\left(x\right) \dx \stackrel{\mathrm{obige\ Eigenschaft}}= -\int_a^a f\left(x\right) \dx \\[4px] \Rightarrow & 2 \int_a^a f\left(x\right) \dx = 0 \\[4px] \Rightarrow & \int_a^a f\left(x\right) \dx = 0\end{align*}](img/248_1988228837_08a409020406a2040604a20409a5a504.png)
Das komplexe Integral ist
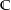 -linear. Das heißt, es ist
-linear. Das heißt, es ist 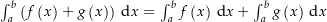 für alle
für alle ![$f,\,g :\ \left[a,\,b\right] \rightarrow \C$](img/45_728063657_a5a3a20906030004a20708a207a30309.png) und
und 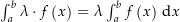 für alle
für alle 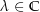 und
und ![$f:\ \left[a,\,b\right]\rightarrow \C$](img/38_125635644_0003a509a204a008a4a3a308a108a309.png) .
.Es gilt für alle
![$f,\,g :\ \left[a,\,b\right] \rightarrow \C$](img/45_728063657_a5a3a20906030004a20708a207a30309.png) Zunächst gilt
Zunächst gilt![\begin{align*}\int_a^b \left(f\left(x\right)+g\left(x\right)\right) \dx & \defeq \int_a^b \Re\left(f\left(x\right)+g\left(x\right)\right) \dx + \i \int_a^b \Im\left(f\left(x\right)+g\left(x\right)\right) \dx \\[4px] & {\color{Orange} \left\downarrow \text{Definition der komplexen Addition} \right.}\\[4px] & = \int_a^b \left(\Re\left(f\left(x\right)\right) +\Re\left(g\left(x\right)\right)\right) \dx \\[4px] & \ + \i \int_a^b \left(\Im\left(f\left(x\right)\right) +\Im\left(g\left(x\right)\right)\right) \dx \\[4px] & {\color{Orange} \left\downarrow \text{Eigenschaft reeller Integrale} \right.}\\[4px] & = \int_a^b \Re\left(f\left(x\right)\right) \dx + \int_a^b \Re\left(g\left(x\right)\right) \dx \\[4px] & \ + \i \left(\int_a^b \Im\left(f\left(x\right)\right)\dx + \int_a^b \Im\left(g\left(x\right)\right) \dx\right) \\[4px] & = \int_a^b \Re\left(f\left(x\right)\right) \dx + \i \int_a^b \Im\left(f\left(x\right)\right) \dx \\[4px] & \ + \int_a^b \Re\left(g\left(x\right)\right)\dx + \i \int_a^b \Im\left(g\left(x\right)\right) \dx \\[4px] & \defeq \int_a^b f\left(x\right) \dx + \int_a^b g\left(x\right) \dx \\[4px]\end{align*}](img/1178_-1760977319_07080307a5a1070601a10503a3a008a1.png) und für alle
und für alle![\begin{align*}\int_a^b \i f\left(t\right) \dt & \defeq \int_a^b \Re\left(\i f\left(t\right)\right) \dt + \i \int_a^b \Im\left(\i f\left(t\right)\right) \dt \\[4px] & = \int_a^b -\Im\left(f\left(t\right)\right) \dt + \i \int_a^b \Re\left(f\left(t\right)\right) \dt \\[4px] & = -\int_a^b \Im\left(f\left(t\right)\right) \dt + \i \int_a^b \Re\left(f\left(t\right)\right) \dt \\[4px] & = \i \left(\i \int_a^b \Im\left(f\left(t\right)\right) \dt + \int_a^b \Re\left(f\left(t\right)\right) \dt\right) \\[4px] & \defeq \i \int_a^b f\left(t\right) \dt \\[4px]\end{align*}](img/583_-893253962_a1a3a0a202a305010807040400a0a5a0.png)
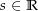 Damit ist für alle
Damit ist für alle![\begin{align*}\int_a^b s\cdot f\left(t\right)\dt &\defeq \int_a^b \Re\left(s\cdot f\left(t\right)\right) \dt + \i \int_a^b \Im\left(s\cdot f\left(t\right)\right) \dt \\[4px] & = \int_a^b s\cdot \Re\left(f\left(t\right)\right) \dt + \i \int_a^b s\cdot \Im\left(f\left(t\right)\right) \dt \\[4px] & = s\cdot \int_a^b \Re\left(f\left(t\right)\right) \dt + \i \cdot s\cdot \int_a^b \Im\left(f\left(t\right)\right) \dt \\[4px] & = s\cdot \left(\int_a^b \Re\left(f\left(t\right)\right) \dt + \i \int_a^b \Im\left(f\left(t\right)\right) \dt\right) \\[4px] & \defeq s\cdot \int_a^b f\left(t\right) \dt \\[4px]\end{align*}](img/633_306970654_07a307090603a507a301a2a4a106a2a0.png)
![$f:\ \left[a,\,b\right]\rightarrow \C$](img/38_125635644_0003a509a204a008a4a3a308a108a309.png) und
und 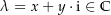
![\begin{align*}\int_a^b \lambda f\left(t\right) \dt & = \int_a^b \left(x+y \cdot \i\right) f\left(t\right) \dt \\[4px] & = \int_a^b \left(x f\left(t\right) + y \i f\left(t\right)\right) \dt \\[4px] & {\color{Orange} \left\downarrow \text{bereits gezeigt: Summe ist rausziehbar} \right.}\\[4px] & = \int_a^b x f\left(t\right) \dt + \int_a^b y \i f\left(t\right) \dt \\[4px] & {\color{Orange} \left\downarrow \text{bereits gezeigt: reelle Zahl ist rausziehbar} \right.}\\[4px] & = x \int_a^b f\left(t\right) \dt + y \int_a^b \i f\left(t\right) \dt \\[4px] & {\color{Orange} \left\downarrow \text{bereits gezeigt: } \i \text{ ist rausziehbar} \right.}\\[4px] & = x \int_a^b f\left(t\right) \dt + y \i \int_a^b f\left(t\right) \dt \\[4px] & = \left(x + y \i\right) \int_a^b f\left(t\right) \dt \\[4px] & = \lambda \int_a^b f\left(t\right) \dt \\[4px]\end{align*}](img/902_1093049217_a0a407a1a3a2a2a1a404000700030102.png)
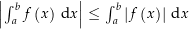
Zum Beweis dieser Eigenschaft verwenden wir die Darstellung von Integralen über Riemansche Zwischensummen. Dabei sei
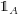 die charakteristische Funktion für die Menge
die charakteristische Funktion für die Menge 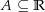 . Damit ist
. Damit ist ![\begin{align*}\amount{\int_a^b f\left(x\right) \dx} & \defeq \amount{\int_a^b \Re\left(f\left(x\right)\right) \dx + \i \int_a^b \Im\left(f\left(x\right)\right) \dx} \\[4px] & {\color{Orange} \left\downarrow \text{Darstellung der beiden Integrale durch Riemannsche Summe} \right.}\\[4px] & = \amount{\limit{\int_a^b \sum_{k=1}^n \Re\left(f\left(\frac{k}{n}\right)\right) \indk \dx} + \i \limit{\int_a^b \sum_{k=1}^n \Im\left(f\left(\frac{k}{n}\right)\right) \indk \dx}} \\[4px] & = \amount{\limit{\sum_{k=1}^n \left(\int_a^b \Re\left(f\left(\frac{k}{n}\right)\right) \indk \dx + \i \int_a^b \Im\left(f\left(\frac{k}{n}\right)\right) \indk \dx\right)}} \\[4px] & = \amount{\limit{\sum_{k=1}^n \int_a^b f\left(\frac{k}{n}\right) \indk \dx}} \\[4px] & {\color{Orange} \left\downarrow \amount{\cdot} \text{ ist stetig} \right.}\\[4px] & = \limit{\amount{\sum_{k=1}^n \int_a^b f\left(\frac{k}{n}\right) \indk \dx}} \\[4px] & {\color{Orange} \left\downarrow \text{Dreiecksungleichung f{\" u}r } \amount{\cdot} \right.}\\[4px] & \le \limit{\sum_{k=1}^n \amount{\int_a^b f\left(\frac{k}{n}\right) \indk \dx}} \\[4px] & {\color{Orange} \left\downarrow f\left(\frac{k}{n}\right) \text{ ist eine Konstante} \right.}\\[4px] & = \limit{\sum_{k=1}^n \amount{f\left(\frac{k}{n}\right)} \amount{\int_a^b \indk \dx}} \\[4px] & {\color{Orange} \left\downarrow \indk \ge 0 \text{ und damit } \int_a^b \indk \dx \ge 0 \right.}\\[4px] & = \limit{\sum_{k=1}^n \amount{f\left(\frac{k}{n}\right)} \int_a^b \indk \dx} \\[4px] & {\color{Orange} \left\downarrow \amount{f\left(\frac{k}{n}\right)} \text{ ist eine Konstante} \right.}\\[4px] & = \limit{\sum_{k=1}^n \int_a^b \amount{f\left(\frac{k}{n}\right)} \indk \dx} \\[4px] & {\color{Orange} \left\downarrow \text{Riemannsche Zwischensumme} \right.}\\[4px] & = \int_a^b \amount{f\left(x\right)} \dx \\[4px]\end{align*}](img/1924_-1428499045_a3a205a4a501a4a40603a300a40107a1.png)