Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Beweise folgende Eigenschaften komplexer Integrale
Ist
![$F:\ \left[a,\,b\right]\rightarrow\C$](img/37_356442910_a40503a4040308a0a202000208080800.png) eine Stammfunktion von
eine Stammfunktion von 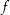 (also
(also 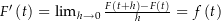 ), so ist
), so ist 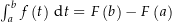
Für diesen Beweis muss (wie du später noch siehst) bewiesen werden, dass
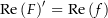 und dass
und dass 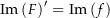 ist. Fangen wir zunächst an,
ist. Fangen wir zunächst an, 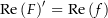 zu beweisen. Es ist Der Beweis, dass
zu beweisen. Es ist Der Beweis, dass![\begin{align*}\Re\left(F\left(t\right)\right)^\prime & = \lim_{h\rightarrow 0} \frac{\Re\left(F\left(t+h\right)\right) - \Re\left(F\left(t\right)\right)}{h} \\[4px] & {\color{Orange} \left\downarrow \text{ nach Definition der komplexen Addition } \right.}\\[4px] & = \lim_{h\rightarrow 0} \frac{\Re\left(F\left(t+h\right) - F\left(t\right)\right)}{h} \\[4px] & {\color{Orange} \left\downarrow \tfrac{1}{h} \text{ ist eine reelle Konstante} \right.}\\[4px] & = \lim_{h\rightarrow 0} \Re\left(\frac{F\left(t+h\right) - F\left(t\right)}{h}\right) \\[4px] & {\color{Orange} \left\downarrow \Re\left(\cdot\right) \text{ ist eine stetige Funktion } \C\rightarrow\R \right.}\\[4px] & = \Re\left(\lim_{h\rightarrow 0} \frac{F\left(t+h\right) - F\left(t\right)}{h}\right) \\[4px] & = \Re\left(F^\prime\left(t\right)\right) = \Re\left(f\left(t\right)\right) \\[4px]\end{align*}](img/902_-1893987447_a2a0a406040003a5a3a308060305a308.png)
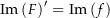 ist, geht analog zur obigen Argumentation (ersetze dabei
ist, geht analog zur obigen Argumentation (ersetze dabei 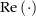 durch
durch 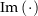 ). Damit ist
). Damit ist ![\begin{align*}\int_a^b f\left(t\right) \dt & = \int_a^b \Re\left(f\left(t\right)\right) \dt + \i \int_a^b \Im\left(f\left(t\right)\right) \dt \\[4px] & {\color{Orange} \left\downarrow \Re\left(F\left(t\right)\right)^\prime = \Re\left(f\left(t\right)\right) \text{ und } \Im\left(F\left(t\right)\right)^\prime = \Im\left(f\left(t\right)\right) \right.}\\[4px] & = \left[\Re\left(F\left(t\right)\right)\right]_a^b + \i \left[\Im\left(F\left(t\right)\right)\right]_a^b \\[4px] & = \Re\left(F\left(b\right)\right) - \Re\left(F\left(a\right)\right) + \i \left(\Im\left(F\left(b\right)\right) - \Im\left(F\left(a\right)\right)\right) \\[4px] & = \Re\left(F\left(b\right)\right) + \i \cdot \Im\left(F\left(b\right)\right) - \left(\Re\left(F\left(b\right)\right) + \i \cdot \Im\left(F\left(b\right)\right)\right) \\[4px] & = F\left(b\right) - F\left(a\right) \\[4px]\end{align*}](img/895_2057103133_a50407a004a1a407a108070107060803.png)