. .

Autor(en)

  • Stephan Kulla ()

Lizenz

Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du

  • das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
  • Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen

Zur Verwendung musst du folgende Bedingungen einhalten:

  • Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.

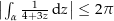
Sei $\alpha:\ \left[0,\,1\right]\rightarrow\C:\ t\mapsto \exp\left(2\pi\i t\right)$. Beweise, dass $\amount{\int_\alpha \frac{1}{4+3z} \dz} \le 2\pi$.

Hinweis zum Lösungsweg

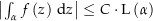
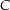
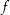
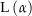
Es ist $\amount{\int_\alpha f\left(z\right) \dz} \le C \cdot\len\left(\alpha\right)$, wobei $\forall t\in\left[0,\,1\right]:\ \amount{f\left(\alpha\left(t\right)\right)} \le C$ (also $C$ eine obere Schranke für den Betrag von $f$ auf $\alpha$) und $\len\left(\alpha\right)$ die Länge von $\alpha$.

Lösungsweg

Es ist


\begin{align*}\amount{4} & = \amount{4+3z-3z} \\[4px] & {\color{Orange} \left\downarrow \text{ Dreiecksungleichung } \right.}\\[4px] & \le \amount{4+3z} + \amount{-3z} = \amount{4+3z} + 3\cdot \underbrace{\amount{z}}_{=\ 1} \\[4px] \Rightarrow\ \amount{4+3z} & \ge \amount{4} - 3\cdot 1 = 1 \\[4px] \Rightarrow\ \frac{1}{\amount{4+3z}} & \le 1 \\[4px] \Rightarrow\ \amount{\frac{1}{4+3z}} & \le 1 \\[4px]\end{align*}

Die Länge $\len\left(\alpha\right)$ der zu integrierenden Kurve $\alpha$ ist gleich $2\pi$ und damit ist


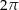
\begin{align*}\amount{\int_\alpha \frac{1}{4+3z} \dz} \le \underbrace{\sup_{t\in\left[0,\,1\right]} \left\{ \amount{\frac{1}{4+3\cdot\alpha\left(t\right)}} \right\}}_{\le\ 1} \cdot \underbrace{\len\left(\alpha\right)}_{=\ 2\pi} \le 2\pi\end{align*}