. .

Autor(en)

  • Stephan Kulla ()

Lizenz

Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du

  • das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
  • Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen

Zur Verwendung musst du folgende Bedingungen einhalten:

  • Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.

Beweisen sie, dass die komplexe Konjugation 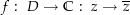$f:\ D\rightarrow\C:\ z\rightarrow\overline z$ auf jeder nichtleeren und offenen Menge 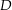$D$ keine holomorphe Stammfunktion besitzt.

Hinweis zum Lösungsweg

Überlege dir: Wie ist der Zusammenhang zwischen der Existenz einer Stammfunktion für 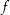$f$ und dem Wert von geschlossen Kurvenintegralen über $f$.

Lösungsweg

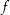Da 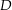$D$ offen und nichtleer ist, existiert in 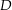$D$ eine offene Kreisscheibe 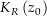$K_R\left(z_0\right)$ mit dem Mittelpunkt 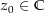$z_0\in\C$ und dem Radius 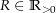$R\in\R_{>0}$. Sei nun 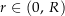$r\in\left(0,\,R\right)$ beliebig. Es ist

\begin{align*}\oint_{\amount{z-z_0}=r} f\left(z\right) \dz & = \oint_{\amount{z-z_0}=r} \overline{z} \dz = \int_0^{2\pi} \overline{r\cdot\exp\left(\i t\right)} r\i\cdot\exp\left(\i t\right) \dt \\[4px] & = r^2 \i \int_0^{2\pi} \underbrace{\exp\left(-\i t\right) \cdot\exp\left(\i t\right)}_{=\,\,1} \dt = r^2 \i \int_0^{2\pi} 1 \dt = 2\pi r^2 \i \ne 0 \\[4px]\end{align*}
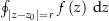Es ist also $\oint_{\amount{z-z_0}=r} f\left(z\right) \dz$ ein geschlossenes Kurvenintegral in 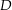$D$ über die Funktion 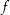$f$, welches nicht Null ist. Damit kann 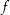$f$ keine holomorphe Stammfunktion besitzen, da sonst jedes geschlossene Kurvenintegral über 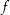$f$ gleich 0 sein müsste.