. .

Autor(en)

  • Stephan Kulla ()

Lizenz

Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du

  • das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
  • Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen

Zur Verwendung musst du folgende Bedingungen einhalten:

  • Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.

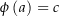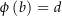Beweise, dass das Kurvenintegral transformationsinvariant ist, dass also gilt: Sei $\alpha:\ \left[c,\,d\right]\rightarrow \C$ eine stückweise glatte Funktion und $f:\ \alpha\left(\left[c,\,d\right]\right)\rightarrow\C$ eine stetige Funktion. Sei nun $\phi:\ \left[a,\,b\right]\rightarrow\left[c,\,d\right]$ eine stetig differenzierbare Funktion mit $\phi\left(a\right)=c$ und $\phi\left(b\right)=d$. Zeige, dass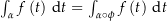 $\int_\alpha f\left(t\right) \dt=\int_{\alpha\circ\phi} f\left(t\right) \dt$

Lösungsweg

Diese Eigenschaft folgt aus der Substitutionsregel für komplexe Integrale. Sei zunächst $\alpha$ eine glatte Kurve. Es ist dann:

\begin{align*}\int_{\alpha\circ\phi} f\left(t\right) \dt & = \int_a^b f\left(\alpha\left(\phi\left(t\right)\right)\right) \alpha^\prime\left(\phi\left(t\right)\right) \phi^\prime\left(t\right) \dt \\[4px] & {\color{Orange} \left\downarrow \text{Substitutionsregel f{\" u}r komplexe Integrale} \right.}\\[4px] & = \int_{\phi\left(a\right)}^{\phi\left(b\right)} f\left(\alpha\left(t\right)\right) \alpha^\prime\left(t\right) \dt \\[4px] & = \int_c^d f\left(\alpha\left(t\right)\right) \alpha^\prime\left(t\right) \dt \\[4px] & = \int_\alpha f\left(t\right) \dt \\[4px]\end{align*}
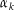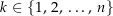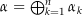Sei nun $\alpha$ stückweise glatt. Dann gibt es glatte Kurven $\alpha_k$ ($k\in\left\{1,\,2,\,\ldots,\,n\right\}$) mit $\alpha=\bigoplus_{k=1}^n \alpha_k$. Es ist dann
\begin{align*}\int_{\alpha\circ\phi} f\left(t\right) \dt & = \int_{\left(\bigoplus_{k=1}^n \alpha_k\right)\circ\phi} f\left(t\right) \dt = \int_{\bigoplus_{k=1}^n \left(\alpha_k\circ\phi\right)} f\left(t\right) \dt \\[4px] & = \sum_{k=1}^n \int_{\alpha_k\circ\phi} f\left(t\right) \dt \\[4px] & = \sum_{k=1}^n \int_{\alpha_k} f\left(t\right) \dt \\[4px] & = \int_{\bigoplus_{k=1}^n \alpha_k} f\left(t\right) \dt = \int_\alpha f\left(t\right) \dt \\[4px]\end{align*}