Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Beweise: Für eine stetige Funktion 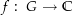 (
(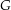 ist ein Gebiet) sind folgende Aussagen äquivalent
ist ein Gebiet) sind folgende Aussagen äquivalent
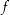 besitzt eine Stammfunktion
besitzt eine Stammfunktion- Jedes Kurvenintegral über
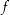 entlang einer geschlossenen Kurve
entlang einer geschlossenen Kurve  in
in 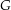 ist gleich
ist gleich 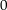 .
. - Jedes Kurvenintegral über
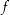 hängt nur vom Anfangs- und Endpunkten ab.
hängt nur vom Anfangs- und Endpunkten ab.
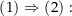 Sei
Sei 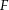 die Stammfunktion von
die Stammfunktion von 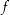 und sei
und sei ![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png) eine beliebige geschlossene Kurve in
eine beliebige geschlossene Kurve in 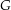 . Es ist dann
. Es ist dann 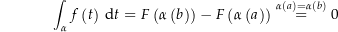
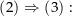 Sei nun jedes geschlossene Kurvenintegral in
Sei nun jedes geschlossene Kurvenintegral in 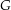 über
über 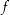 gleich 0. Zu zeigen ist, dass
gleich 0. Zu zeigen ist, dass 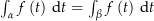 für alle (stückweise glatten) Kurven
für alle (stückweise glatten) Kurven ![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png) und
und ![$\beta:\ \left[c,\,d\right]\rightarrow\C$](img/41_-94824748_08a0a4a2a10109a507a004070002a500.png) mit
mit 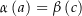 und
und 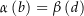 . Sei nun also
. Sei nun also ![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png) und
und ![$\beta:\ \left[c,\,d\right]\rightarrow\C$](img/41_-94824748_08a0a4a2a10109a507a004070002a500.png) zwei stückweise glatte Kurven mit
zwei stückweise glatte Kurven mit 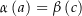 und
und 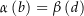 . Es ist dann
. Es ist dann 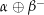 eine stückweise glatte und geschlossene Kurve und damit
eine stückweise glatte und geschlossene Kurve und damit ![\begin{align*}& \int_{\alpha\oplus\beta^{-}} f\left(t\right) \dt \stackrel{\alpha\oplus\beta^{-} \mathrm{\ ist\ geschlossen}}= 0 \\[4px] \Rightarrow & \int_\alpha f\left(t\right) \dt + \int_{\beta^{-}} f\left(t\right) \dt = 0 \\[4px] \Rightarrow & \int_\alpha f\left(t\right) \dt - \int_{\beta} f\left(t\right) \dt = 0 \\[4px] \Rightarrow & \int_\alpha f\left(t\right) \dt = \int_{\beta} f\left(t\right) \dt \\[4px]\end{align*}](img/441_-1707535438_a205a1060303030201a40006a400a008.png)
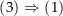 : Sei zunächst
: Sei zunächst 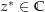 ein beliebeiger Punkt aus
ein beliebeiger Punkt aus 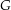 . Da
. Da 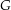 ein Gebiet und damit kurvenzusammenhängend ist, kann jeder Punkt
ein Gebiet und damit kurvenzusammenhängend ist, kann jeder Punkt  aus
aus 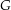 mit
mit 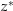 durch eine Kurve verbunden werden. Wir definieren nun Da (wie bereits erwähnt) jeder Punkt in
durch eine Kurve verbunden werden. Wir definieren nun Da (wie bereits erwähnt) jeder Punkt in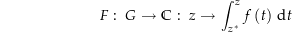
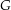 mit
mit 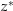 durch eine Kurve verbunden ist und das Integral
durch eine Kurve verbunden ist und das Integral 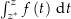 nur vom Anfangs- und Endpunkt abhängig ist, ist die obige Definition wohldefiniert.
Sei nun
nur vom Anfangs- und Endpunkt abhängig ist, ist die obige Definition wohldefiniert.
Sei nun 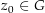 beliebig. Zu zeigen ist:
beliebig. Zu zeigen ist: 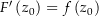 (wobei hier die komplexe Ableitbarkeit gemeint ist). Es muss also gelten Da
(wobei hier die komplexe Ableitbarkeit gemeint ist). Es muss also gelten Da![\begin{align*}& F\left(z\right) = F\left(z_0\right) + f\left(z_0\right) \left(z-z_0\right) + r\left(z\right),\, \lim_{z\rightarrow z_0} \frac{r\left(z\right)}{z-z_0} = 0 \\[4px] \Leftrightarrow & \int_\z^z f\left(t\right) \dt = \int_\z^{z_0} f\left(t\right) \dt + f\left(z_0\right) \left(z-z_0\right) + r\left(z\right),\, \lim_{z\rightarrow z_0} \frac{r\left(z\right)}{z-z_0} = 0 \\[4px] \Leftrightarrow & \underbrace{\int_\z^z f\left(t\right) \dt - \int_\z^{z_0} f\left(t\right) \dt}_{\int_{z_0}^z f\left(t\right) \dt} - f\left(z_0\right) \left(z-z_0\right) = r\left(z\right),\, \lim_{z\rightarrow z_0} \frac{r\left(z\right)}{z-z_0} = 0 \\[4px] \Leftrightarrow & \lim_{z\rightarrow z_0} \frac{\int_{z_0}^z f\left(t\right) \dt - f\left(z_0\right)\left(z-z_0\right)}{z-z_0} = 0 \\[4px]\end{align*}](img/808_1362991013_a4000306a103020808a504060205a3a1.png)
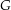 ein Gebiet ist, ist
ein Gebiet ist, ist 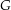 nach Definition offen und es gibt eine offene Kreisscheibe
nach Definition offen und es gibt eine offene Kreisscheibe 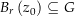 mit
mit 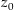 als Mittelpunkt und
als Mittelpunkt und 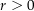 als Radius. Diese Kreisscheibe ist ein Sterngebiet und wir können hier
als Radius. Diese Kreisscheibe ist ein Sterngebiet und wir können hier  und
und 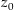 direkt verbinden, um das Integral
direkt verbinden, um das Integral 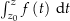 zu berechnen. Die Dirketverbindung von
zu berechnen. Die Dirketverbindung von 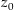 zu
zu  ist die glatte Kurve
ist die glatte Kurve ![$\alpha:\ \left[0,\,1\right]\rightarrow\C:\ t\rightarrow z_0 + t\left(z-z_0\right)$](img/83_1767744889_0708a2a505a0050206050602020809a2.png) . Es ist Zu zeigen ist also, dass
. Es ist Zu zeigen ist also, dass![\begin{align*}\lim_{z\rightarrow z_0} \frac{\int_{z_0}^z f\left(t\right) \dt - f\left(z_0\right)\left(z-z_0\right)}{z-z_0} & = \lim_{z\rightarrow z_0} \frac{\int_\alpha f\left(t\right) \dt - f\left(z_0\right)\left(z-z_0\right) \overbrace{\int_0^1 1 \dt}^{=\ 1}}{z-z_0} \\[4px] & = \lim_{z\rightarrow z_0} \frac{\int_0^1 f\left(z_0 + t\left(z-z_0\right)\right) \left(z-z_0\right) \dt - \int_0^1 f\left(z_0\right)\left(z-z_0\right) \dt}{z-z_0} \\[4px] & = \lim_{z\rightarrow z_0} \frac{\int_0^1 f\left(z_0 + t\left(z-z_0\right)\right) \left(z-z_0\right) - f\left(z_0\right)\left(z-z_0\right) \dt}{z-z_0} \\[4px] & = \lim_{z\rightarrow z_0} \int_0^1 \frac{f\left(z_0 + t\left(z-z_0\right)\right) \left(z-z_0\right) - f\left(z_0\right)\left(z-z_0\right)}{z-z_0} \dt \\[4px] & = \lim_{z\rightarrow z_0} \int_0^1 \left(f\left(z_0 + t\left(z-z_0\right)\right) - f\left(z_0\right)\right) \dt \\[4px]\end{align*}](img/919_33363570_05a3a2020008a5a10003080308080202.png)
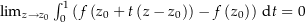 ist. Nun ist
ist. Nun ist 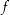 eine stetige Funktion ist. Es gibt also für alle
eine stetige Funktion ist. Es gibt also für alle 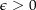 ein
ein 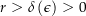 , so dass für alle
, so dass für alle 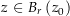 mit
mit 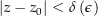 die Ungleichung
die Ungleichung 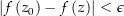 erfüllt ist. Es ist dann Damit ist
erfüllt ist. Es ist dann Damit ist![\begin{align*}\amount{\int_0^1 \left( f\left(z_0+t\left(z-z_0\right)\right) -f\left(z_0\right) \right) \dt} & \le \int_0^1 \underbrace{\amount{f\left(z_0+t\left(z-z_0\right)\right) -f\left(z_0\right)}}_{\le\,\,\epsilon} \dt \\[4px] & \le \int_0^1 \epsilon \dt = \epsilon \int_0^1 1 \dt = \epsilon \\[4px]\end{align*}](img/320_135777760_060909030407a50709a2a40805a403a0.png)
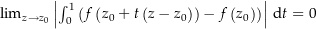 , also auch
, also auch 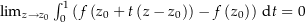 .
.