Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
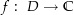
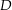
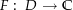
![$\alpha:\ \left[a,\,b\right]\rightarrow\C$](img/42_-2027026022_0407a407a1a203a0070607a1040409a2.png)
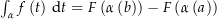
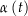
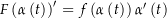
![\begin{align*}\int_\alpha f\left(t\right) \dt & = \int_a^b f\left(\alpha\left(t\right)\right) \alpha^\prime\left(t\right) \dt = \left[F\left(\alpha\left(t\right)\right)\right]_a^b \\[4px] & = F\left(\alpha\left(b\right)\right) - F\left(\alpha\left(a\right)\right) \\[4px]\end{align*}](img/287_-1944088922_05a406a504a0a302a006a20508050904.png)