Quelle der Aufgabe
Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 68
Autor(en)
- Stephan Kulla ()
Lizenz
Dieses Werk von Stephan Kulla steht unter einer „Creative Commons Namensnennung 3.0 Deutschland-Lizenz“. Damit darfst du
- das Werk bzw. den Inhalt vervielfältigen, verbreiten und öffentlich zugänglich machen
- Abwandlungen und Bearbeitungen des Werkes bzw. Inhaltes anfertigen
Zur Verwendung musst du folgende Bedingungen einhalten:
- Namensnennung - Du musst den Autor/die Autoren nennen und ein Link auf dieses Werk setzen.
Berechne das Kurvenintegral 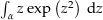 , wenn (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 68)
, wenn (Quelle der Aufgabe: Buch „Funktionentheorie 1“ von Eberhard Freitag und Rolf Busam, Auflage 3, 2000, ISBN 3-540-67641-4, Seite 68)
 die Verbinungssterecke zwischen
die Verbinungssterecke zwischen 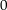 und
und 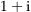 ist.
ist.Wenn
 die Verbinsungsstrecke zwischen
die Verbinsungsstrecke zwischen 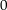 und
und 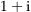 ist, so kann man
ist, so kann man  als glatte Kurve
als glatte Kurve ![$\alpha:\ \left[0,\,1\right]\rightarrow\C:\ t\rightarrow t\cdot\left(1+\i\right)$](img/81_-136052566_05a2a409a5a109a50303a10500a20602.png) definieren. Es ist dann
definieren. Es ist dann ![\begin{align*}\int_\alpha z \exp\left(z^2\right) \dz & = \int_0^1 \alpha\left(t\right) \exp\left(\alpha\left(t\right)^2\right) \alpha^\prime\left(t\right) \dt \\[4px] & = \int_0^1 t \left(1+\i\right) \exp\left(t^2 \left(1+\i\right)^2\right) \left(1+\i\right) \dt \\[4px] & = \int_0^1 t \left(1+\i\right)^2 \exp\left(t^2 \left(1+\i\right)^2\right) \dt \\[4px] & = \frac{1}{2} \int_0^1 2 t \left(1+\i\right)^2 \exp\left(t^2 \left(1+\i\right)^2\right) \dt \\[4px] & {\color{Orange} \left\downarrow \left(\exp\left(t^2 \left(1+\i\right)^2\right)\right)^\prime = 2 t \left(1+\i\right)^2 \exp\left(t^2 \left(1+\i\right)^2\right) \right.}\\[4px] & = \frac{1}{2} \left[\exp\left(t^2 \left(1+\i\right)^2\right)\right]_0^1 \\[4px] & = \frac{1}{2} \left(\exp\left(1^2 \left(1+\i\right)^2\right) - \exp\left(0^2 \left(1+\i\right)^2\right)\right) = \frac{1}{2}\left(\exp\left(\left(1+\i\right)^2\right)-1\right) \\[4px] & = \frac{1}{2}\left(\exp\left(2\i\right) - 1\right) \\[4px]\end{align*}](img/1014_-383685542_04a1a0a1a2a004040805a30508a3a204.png)
Es ist
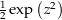 eine holomorphe Funktion mit der Ableitung
eine holomorphe Funktion mit der Ableitung 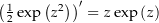 . Damit ist
. Damit ist ![\begin{align*}\int_\alpha z \exp\left(z^2\right) \dz & = \left[\frac{1}{2} \exp\left(z^2\right)\right]_{\alpha\left(0\right)}^{\alpha\left(1\right)} \\[4px] & = \frac{1}{2} \exp\left(\alpha\left(1\right)^2\right) - \frac{1}{2} \exp\left(\alpha\left(0\right)^2\right) \\[4px] & = \frac{1}{2}\left(\exp\left(\left(1+\i\right)^2\right) - \exp\left(0^2\right)\right) = \frac{1}{2}\left(\exp\left(2\i\right) - 1\right) \\[4px]\end{align*}](img/443_1669455626_040707a200a500a504a0a3a308a20405.png)
 die Verbindungsstrecke auf der Parabel von
die Verbindungsstrecke auf der Parabel von 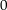 bis
bis 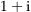 ist
istSchau dir mal den zweiten Lösungsweg zur ersten Aufgabe an
Diese Aufgabe lässt sich analog zur ersten Teilaufgabe lösen (siehe 2. Lösungsweg der ersten Teilaufgabe - der Lösungsweg ist identisch). Damit ist auch hier
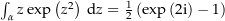
Bedenke, dass geschlossene Kurven über Funktionen mit analytischer Stammfunktion stets 0 ist.
Sei
![$\alpha:\ \left[0,\,1\right]\rightarrow\C:\ t\rightarrow t+t^2\i$](img/65_588318139_06a5090900030600a20608a404090508.png) die Parabelkurve zwischen
die Parabelkurve zwischen 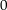 und
und 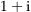 . Sei
. Sei ![$\beta:\ \left[0,\,1\right]\rightarrow\C:\ t\rightarrow t\left(1+\i\right)$](img/75_-114273500_070201a206050609a007a5000101a009.png) die direkte Verbindungsstrecke zwischen
die direkte Verbindungsstrecke zwischen 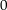 und
und 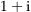 . Dann ist
. Dann ist 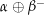 eine geschlossene Kurve (
eine geschlossene Kurve (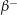 ist dabei die reziproke Kurve von
ist dabei die reziproke Kurve von 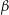 ). Da
). Da 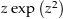 eine Stammfunktion besitzt (nämlich die Funktion
eine Stammfunktion besitzt (nämlich die Funktion 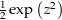 ), ist jedes Kurvenintegral mit einer geschlossenen Kurve und über diese Funktion gleich
), ist jedes Kurvenintegral mit einer geschlossenen Kurve und über diese Funktion gleich 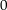 . Damit ist
. Damit ist ![\begin{align*}& \int_{\alpha\oplus\beta^{-}} z \exp\left(z^2\right) \dz = 0 \\[4px] \Rightarrow\ & \int_\alpha z\exp\left(z^2\right) \dz + \int_{\beta^{-}} z\exp\left(z^2\right) \dz = 0 \\[4px] \Rightarrow\ & \int_\alpha z\exp\left(z^2\right) \dz - \int_{\beta} z\exp\left(z^2\right) \dz = 0 \\[4px] \Rightarrow\ & \int_\alpha z\exp\left(z^2\right) \dz = \int_{\beta} z\exp\left(z^2\right) \dz \\[4px] & {\color{Orange} \left\downarrow \text{ Teilaufgabe 1} \right.}\\[4px] \Rightarrow & \int_\beta z\exp\left(z^2\right) \dz = \frac{1}{2}\left(\exp\left(2\i\right) - 1\right) \\[4px]\end{align*}](img/620_-878540666_08030903a000a508a4a2040408a30804.png)